《对数函数的图像与性质》的教学新设计
佛山市第四中学 彭晓燕
华南师范大学数学科学学院 何小亚
为了提高佛山市高中数学教学水平,佛山市教育局教研室彭海燕副主任邀请我们为全
区的高中数学教师做一个基于高中数学新课标和新教材的教学设计示范案例,并于 2019 年
10 月 17 日上午在佛山市第四中学面向全区的高中数学科组长和骨干教师上了公开示范课,
引发了大家的热议.以下是我们根据追求数学素养的教学设计标准
[1]、[2]
设计的教案和反思,
希望广大读者批评指正.
1.教案设计
【教材】人教 A 版(2007)普通高中数学必修一 2.2.2【课时安排】第 1 课时
【教材分析】将复杂的函数问题化归为简单的基本初等函数问题,是研究函数的核心
思路.对数函数就是一种重要的基本初等函数.本节内容是在学习对数的概念和运算性质后,
进一步学习对数函数的定义、图像、性质及初步应用.对数函数的图像与性质的学习过程与
指数函数部分的学习类似,注重学生参与探究的过程,因此可以类比进行教学.
【学情分析】
1. 认知基础:学生已学习了指数函数的概念和图像,对数概念,积累了探究指数函数
性质的经验.这些是学习对数函数概念及其性质的基础.
2.认知障碍:函数概念的本质;指数函数与对数函数互为反函数的理解;容易忽略底
数
a
对图象的影响.
【教学目标】
1.知识与技能
(1
)理解对数函数的定义,深刻认识函数的本质
(
具体内容见问题 2 之后
)
;熟悉指
数函数、对数函数的增长快慢的差异;知道指数函数与对数函数互为反函数
.
(2)掌握对数函数的图象和性质,会用其比较对数的大小.
2. 过程与方法
(1)通过问题 2 和 3 的讨论过程,提高学生的函数素养;
(2)通过问题 4 的提出、分析、解决过程,进一步强化应用函数模型解决特殊问题的
一般化思想和问题解决中的化归思想.
3. 情感态度与价值观
(1)让学生喜欢对数、对数函数;
(2)感受对数运算强大的简化、压缩功能;
(3)感受指数函数、幂函数
y=x
、对数函数增长快慢的巨大差异.
【教学重点】对数函数的定义和性质.
【教学难点】1.指数函数与对数函数互为反函数;2.底数
a
的大小与函数图象变化.
【关键】利用对数和指数的互逆关系和解释函数概念的本质突破难点 1;利用几何画
板直观演示底数
a
的变化对函数图像的影响来突破难点 2.
【教学方法】问题驱动、概念同化、引导探究.教学手段:PPT、几何画板.
1
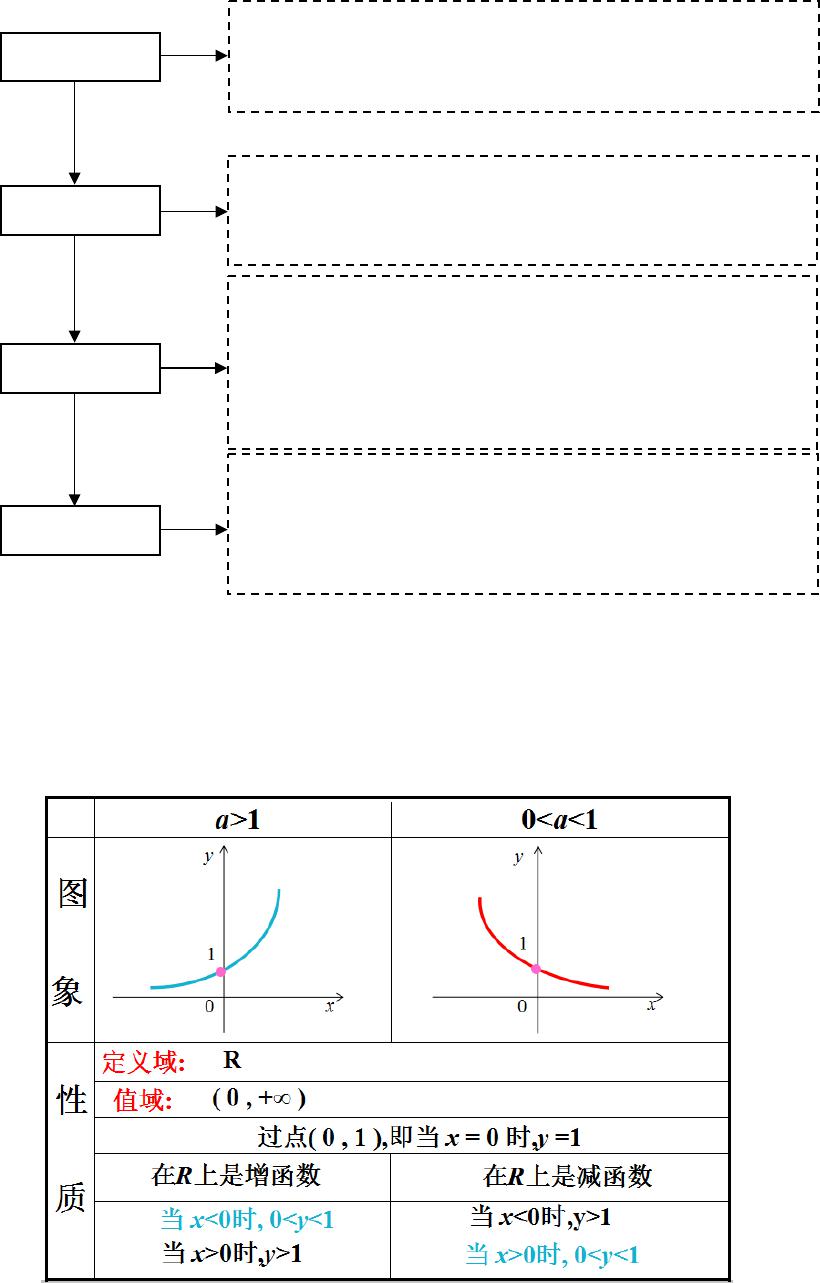
【教学流程设计】
【教学过程设计】
(一)问题引入(10 分钟)
问题 1:什么叫做指数函数,它有什么性质?
教师引导学生回答并显示表格内容.
问题 2:什么是函数,你看清楚了函数的真面目吗?
问题引入
探究发现
巩固应用
小结及作业
设计意图:通过对函数的定义的剖析得到对数函数,
加深对函数定义的理解,也有助于学生形成系统的知
识结构,体会知识的融会贯通.
设计意图:学生在探究对数函数图像的过程中,充分
体会从特殊到一般的过程,从而得到对数函数的图像,
并类比指数函数的探究方法,得到对数函数的性质.
设计意图:学生通过求函数定义域,加深对对数函数
的理解;通过比较两个同底对数的大小,熟悉对数的性
质.并通过指数函数、幂函数、对数函数增长快慢的
巨大差异,感受对数运算强大的简化、压缩功能.
设计意图:小结意在巩固本节课所学知识,回顾探索
历程,学习数学思想;并通过“无穷酒杯”的形象比
喻,使学生对函数图像的理解更直观,更深刻.作业
意在使学生进一步熟悉对数函数的图像及其性质.
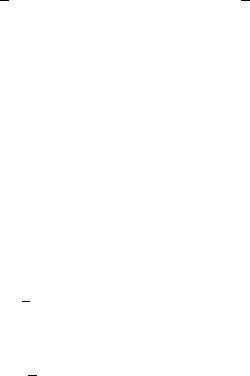
2
教师指着指数函数紧扣其解释:函数是两个非空数集之间的一种对应关系;在一个集
合中任意取定一个数,总可以在另一个集合里找到唯一确定的数与它对应;前面的集合叫
定义域,那些被唯一确定的所有数组成了叫做值域的集合;函数概念的关键是由谁唯一确
定了谁;函数概念与两个变量所用的符号没有什么关系,就像人的名字一样(圆面积
S
是
半径
r
的函数,这里并没有
x
、
y
);函数其实就是一个系统,一台机器,它由两个变量,
两个非空数集,对应法则
f
(比如乘 2 加 3,平方,表格对应,箭头对应,……)构成,不能
把函数值
f
(
x
)当成函数,也不能把对应法则
f
当成函数.我们可以说一个变量是另一个变量
的函数,但不能把变量
x
、
y
当成函数,因为函数不是变量,而是一个系统.
问题 3:已知指数函数
x
ay =
,请问变量
x
是否是
y
的函数?
师生一起验证其符合函数的定义,
x
是
y
的函数,因为由指数函数的图像和性质可知,
y
的每一个取值,都能找到唯一的
x
与之对应.对应关系是
yx
a
log=
,
( )
+∞∈ ,0y
.最后
给出对数函数的定义. 为了在同一坐标系下研究不同函数的性质,我们通常用
x
表示自变
量
,y
表示函数,形如
xy
a
log=
(
1
0
≠>
a
a 且
)的函数叫做对数函数.定义域为
( )
∞+,0
.
【设计意图】通过对函数的定义的剖析得到对数函数,加深对函数定义的理解,也有助
于学生形成系统的知识结构,体会知识的融会贯通.
(二)探究发现(15 分钟)
问题 4:不用查表,不用计算器,能否知道下列各组数中哪一个大?
5.8log,4.3log1
5.05.0
)(
)且()( 105.8log,4.3log2 ≠> aa
aa
教师活动:第二组数即使是对数表也不能派上用场.我们在学习指数函数时,学到了一
种重要的数学思想:一般化!即:面对两个具体的数值大小比较难题,我们把问题一般化,
将它们看成是某一函数的两个函数值,利用函数的单调性就可以判断谁大谁小!
要想解决这两个难题,我们先来研究对数函数的图像和性质.
问题 5:请在同一坐标系上画出对数函数的图像,教师引导学生分两组合作,分别画出
xyxyxyxy
3
13
2
12
loglogloglog ==== 和,和
的图像,
问题 6:每一组图像有什么特点?
展示学生的成果并观察图像,引导学生得出图像特点:
①图象都在
y
轴右侧;
②都过点(1,0),即
01log =
a
;
③当
a
>1 时,图象沿
x
轴正向逐步上升;当
01a<<
时,图象沿
x
轴正向逐步下降.
④
xyxy
2
12
loglog == 与
图像关于
x
轴对称.
(为什么?因为
xx
y
2
2
1
loglog −=
=
)
问题 7:对数函数的图像有哪些典型的类别?
3
学生活动:思考问题并进行猜想.
教师活动:肯定学生的发现,并利用几何画板,选取底数
a
0( >a
,且
)
1
≠
a
的若干个不
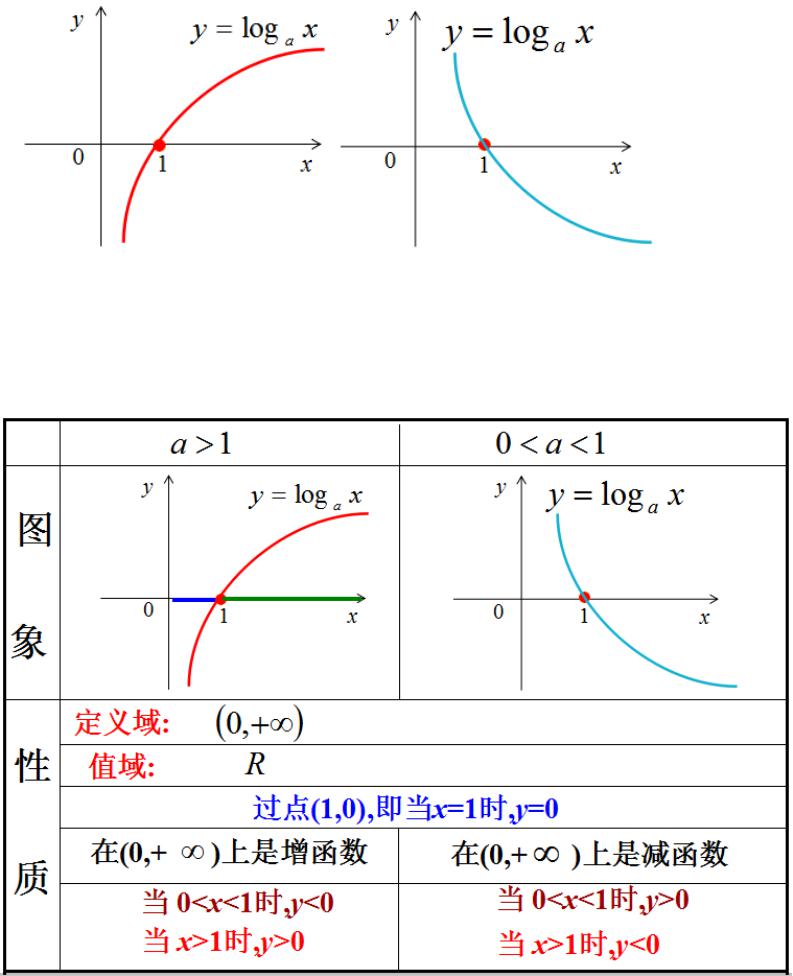
同的值,在同一平面直角坐标系中作出相应对数函数的图象,归纳出以下图像.
)1(log >= ax
y
a
( )
10log <<= axy
a
类比指数函数,我们可以根据图象特征探究出对数函数的定义域、值域、单调性、对
称性、过定点等性质,完善以下表格.
【设计意图】学生在探究对数函数图像的过程中,充分体会从特殊到一般的过程,从而
得到对数函数的图像,并类比指数函数的探究方法,得到对数函数的性质.
(三)巩固应用(10 分钟)
例 1.
求函数
( )
.)10(4log 的定义域且 ≠>−= aaxy
a
根据真数大于 0,教师引导学生口答并示范板演.
例 2.
分别比较大小:
5.8log,4.3log
1
5.05.0
)(
;
)
且()( 105.8log
,4.3log2 ≠> aa
aa
.
4
( )
5.8log4
.3log
5.84.3,0
log5.8log4.3log1
5.05.0
5.05.05
.0
<∴
<+∞
=
上是减函数,且而此函数在
的两个函数值,可以看成函数和)(
xy
( )
( )
.5.8log4.3log
,5.84.3,0log10
.5.8log4.3log
,5.84.3,0log1
log5.8log4.3log2
aa
a
aa
a
aaa
xya
xya
xy
>
∴
<+∞=<<
<
∴
<+∞=>
=
上是减函数,且在函数时,
当
上是增函数,且在函数时,
当
的两个函数值,可以看成函数和)
(
教师活动:引导学生口答,并由教师示范板演.
小结:比较同底数的两个对数的大小,可利用对数函数的单调性,要注意底数的范围.
学生活动:牛刀小试.
的定义域为)函数(
x
y
31
1
log1
7
−
=
;
的定义域为函数
x
y
2
log
1
=
.
.
,,loglog
3
3.0
3.0
的大小
比较)已知
( nm
nm >
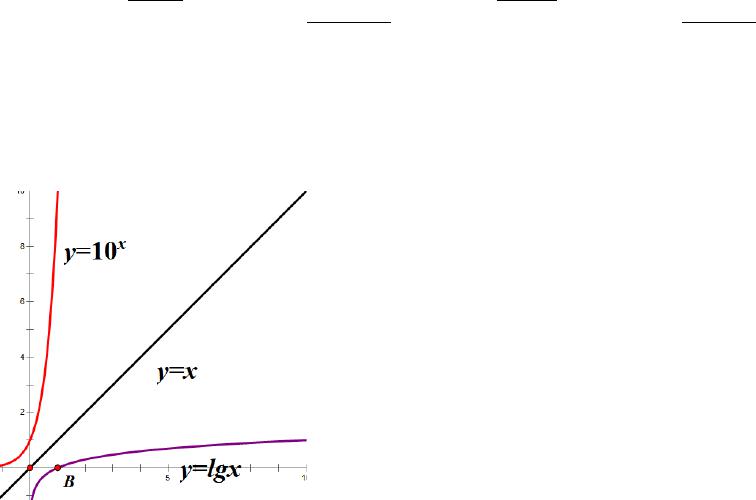
问题 8:随着 x 的无限增大,三个函数
y=
10
x
,y=x,y=
lg
x
的函数值
y
的大小关系是什
么?
教师活动:1.几何画板显示图像,直接指出三个函数值的大小顺序;
2.引导学生口算:当
x
取 0.001,0.01,0.1,1,10,100,1000,…,一千万时,常
用对数函数值分别是-3,-2,-1,0,1,2,3,…,7 来说明
y=
lg
x
几乎是贴着
x
轴增长
到无穷大的.
教师总结:看到没有,一个如此疯狂大的数,一旦被取对数后就被压缩得如此之小!
在数学家眼里,取对数就是一台功能强大的压缩机!我好喜欢,好宠爱,好膜拜这台疯狂
的压缩机!同学们,你呢?
3.看图像,下结论:
