搜索'微演示',好用的pdf转网页工具
阻尼动力吸振器
The damped dynamic vibration absorbers
汇报人：林锦鑫
2025 年 11 月 25 日
林锦鑫 Damped DVA 2025 年 11 月 25 日 1 / 19
目录
1
引言
2
Model A (经典模型) 回顾
3
扰动法求最佳阻尼比
4
微分法求最佳阻尼比
5
结果与总结
林锦鑫 Damped DVA 2025 年 11 月 25 日 2 / 19
引言 (Introduction)
DVA (Dynamic Vibration Absorber) 简介
DVA 用于抑制主系统在共振频率下的振动。然而，无阻尼 DVA 会引入两个新
的共振峰，因此必须加入阻尼器以优化性能。
两种模型构型
Model A (经典): 阻尼器连接主质量 m 和吸振器
质量 m
a
。
Model B (本文重点): 阻尼器连接吸振器质量 m
a
和地（惯性参考系），类似”Groundhook” 阻尼。
图 1: DVA 模型对比
林锦鑫 Damped DVA 2025 年 11 月 25 日 3 / 19
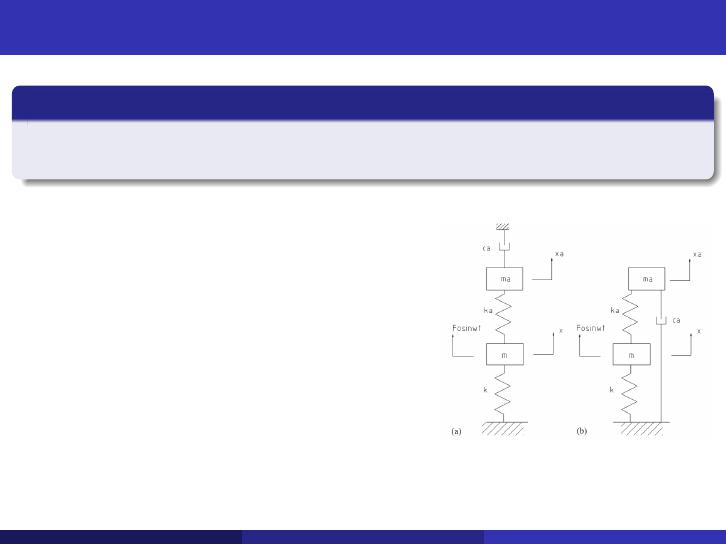
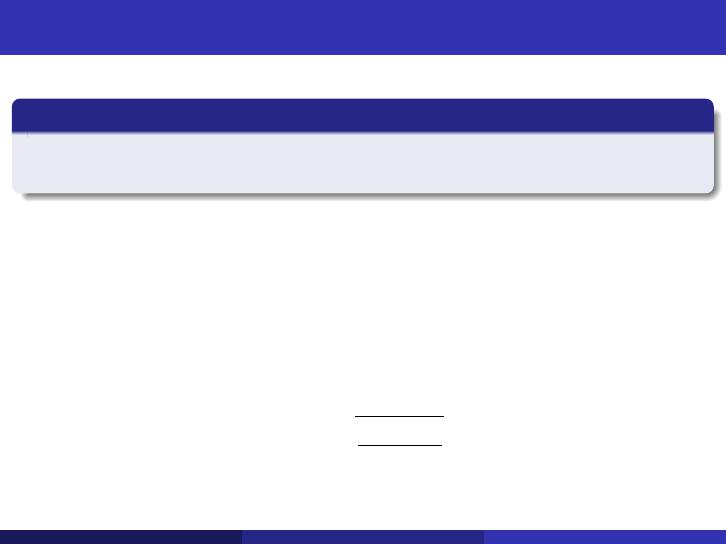
Model A (经典模型) 的回顾
运动方程
m
¨
x + c
a
˙
x − c
a
˙
x
a
+ (k + k
a
)x − k
a
x
a
= F
0
sin(ωt)
m
a
¨
x
a
− c
a
˙
x + c
a
˙
x
a
− k
a
x + k
a
x
a
= 0
归一化振幅 G
G =




Xk
F
0




=
s
(2ζr)
2
+ (β
2
− r
2
)
2
[1 − (1 + µ)r
2
]
2
(2ζr)
2
+ [(1 − r
2
)(β
2
− r
2
) − µβ
2
r
2
]
2
参数定义: µ = m
a
/m (质量比), β = ω
a
/ω
p
(频率比), ζ = c
a
/(2mω
p
) (阻尼比),
r = ω/ω
p
(激励频率比)。
林锦鑫 Damped DVA 2025 年 11 月 25 日 4 / 19
Model A 的优化困境与 Brock 方法
Den Hartog 的定点理论
存在两个与阻尼无关的固定点 P 和 Q。使 P、Q 等高的条件给出了最优频率比:
β = 1/(1 + µ)。
最优阻尼比的推导难题
直接求导方法面临巨大挑战：Den Hartog 建议对 ∂G/∂r 求导，计算量过大。在
汇报第二篇文献时会进行介绍
解决方案: 使用 Brock 的微扰法 (Perturbation approach)，无需直接微分，巧妙
规避了复杂的代数运算。
求出最佳阻尼比 ζ
opt
ζ
opt
=
s
3µ
8 (1 + µ)
3
林锦鑫 Damped DVA 2025 年 11 月 25 日 5 / 19