
1
阻尼动力吸振器公式推导

汇报人:林锦鑫
汇报日期:2025.12.15

目录
2
01
阻尼动力吸振器
02
最佳频率比
03
最佳阻尼比
04
Matlab程序
05
导数法的补充

1.1 阻尼动力吸振器
3
无阻尼动力吸振器
阻尼动力吸振器
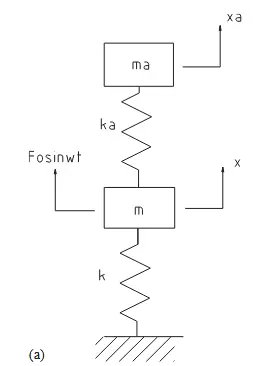
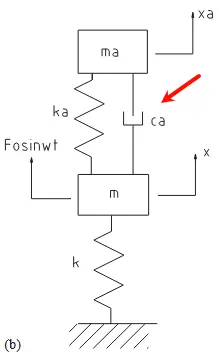
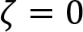
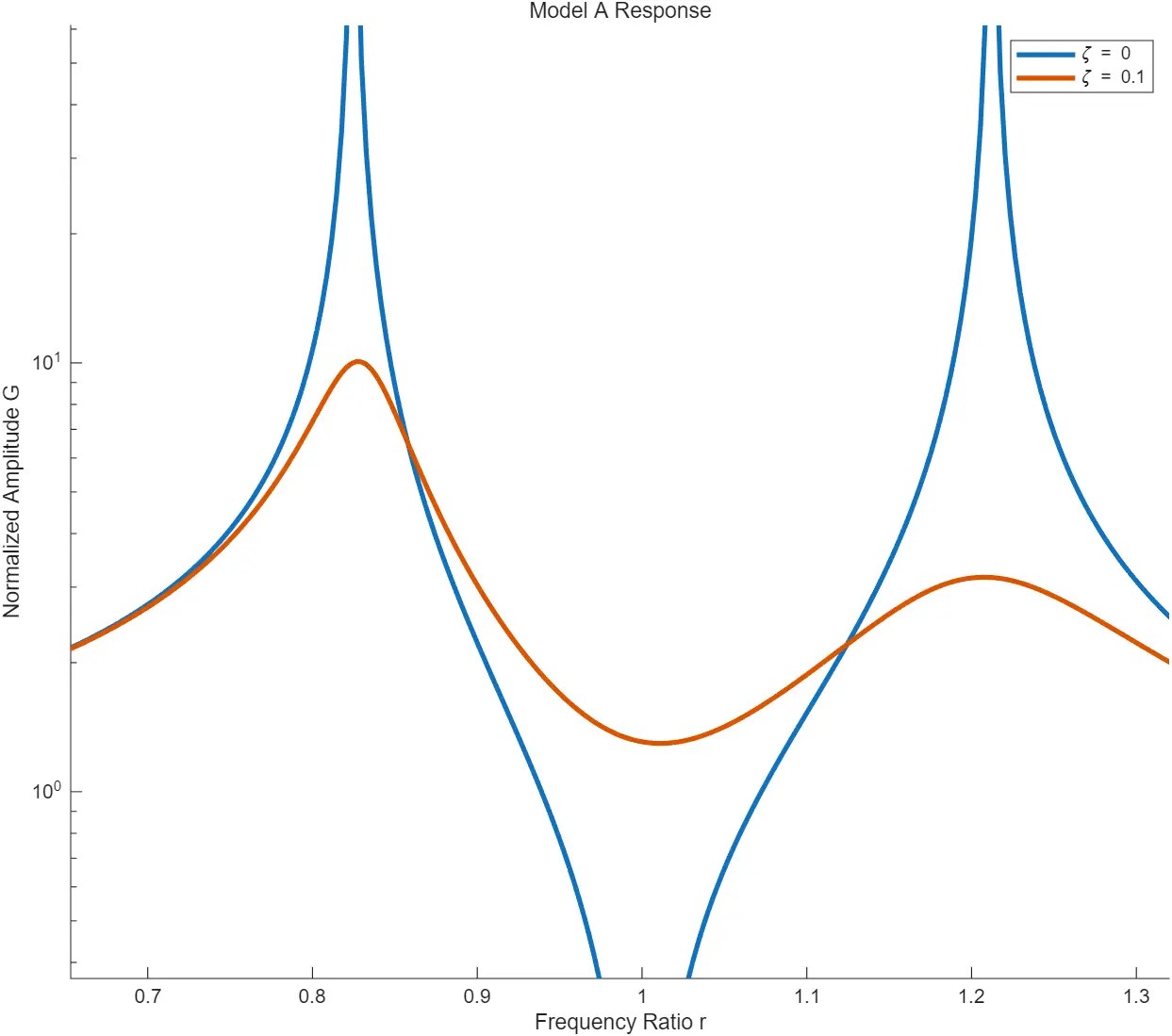
二者的幅频特性曲线


1.2 模型介绍
4
经典模型
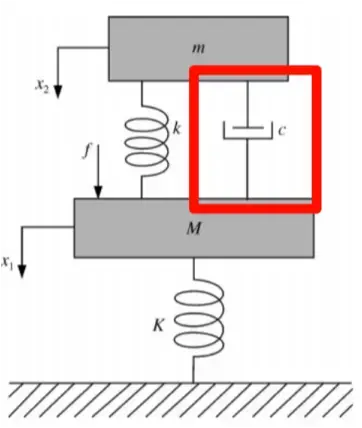
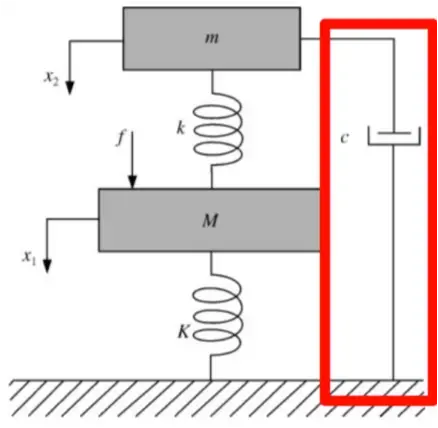
地钩模型
研究方法
研究目的
理论推导


最优条件下,两个模型的吸振能力对比
最优参数
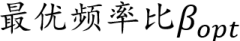
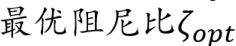
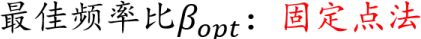

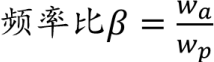
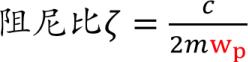

目录
5
01
阻尼动力吸振器
02
最佳频率比
03
最佳阻尼比
04
Matlab程序
05
导数法的补充

2.1 稳态响应求解(1/2)
6
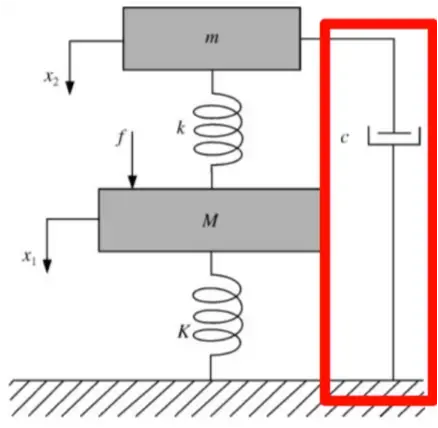
地钩模型
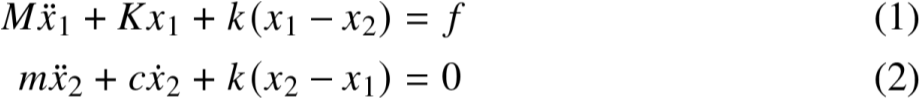
对两个质量块列运动微分方程,有以下式子
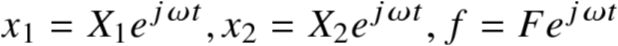
采用复数法,化简微分方程
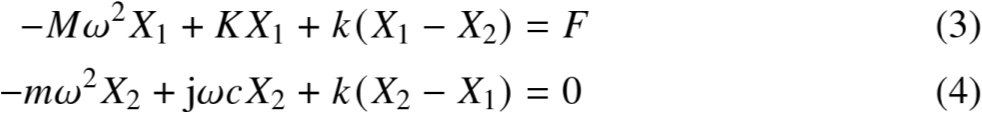
得到一个简单的代数方程

2.1 稳态响应求解(2/2)
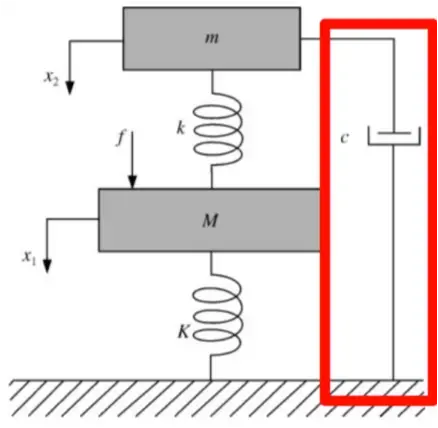
地钩模型
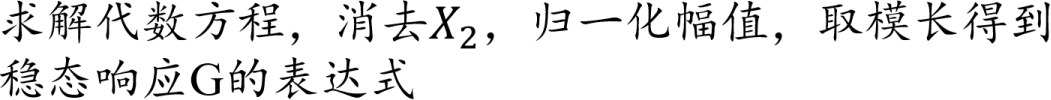
参数说明
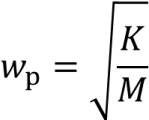
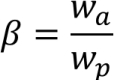
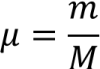

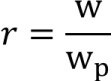
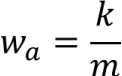
7
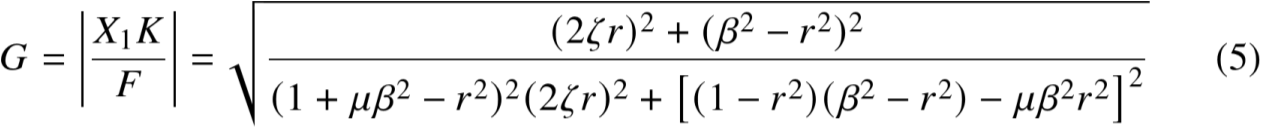

2.2 幅频特性曲线
8
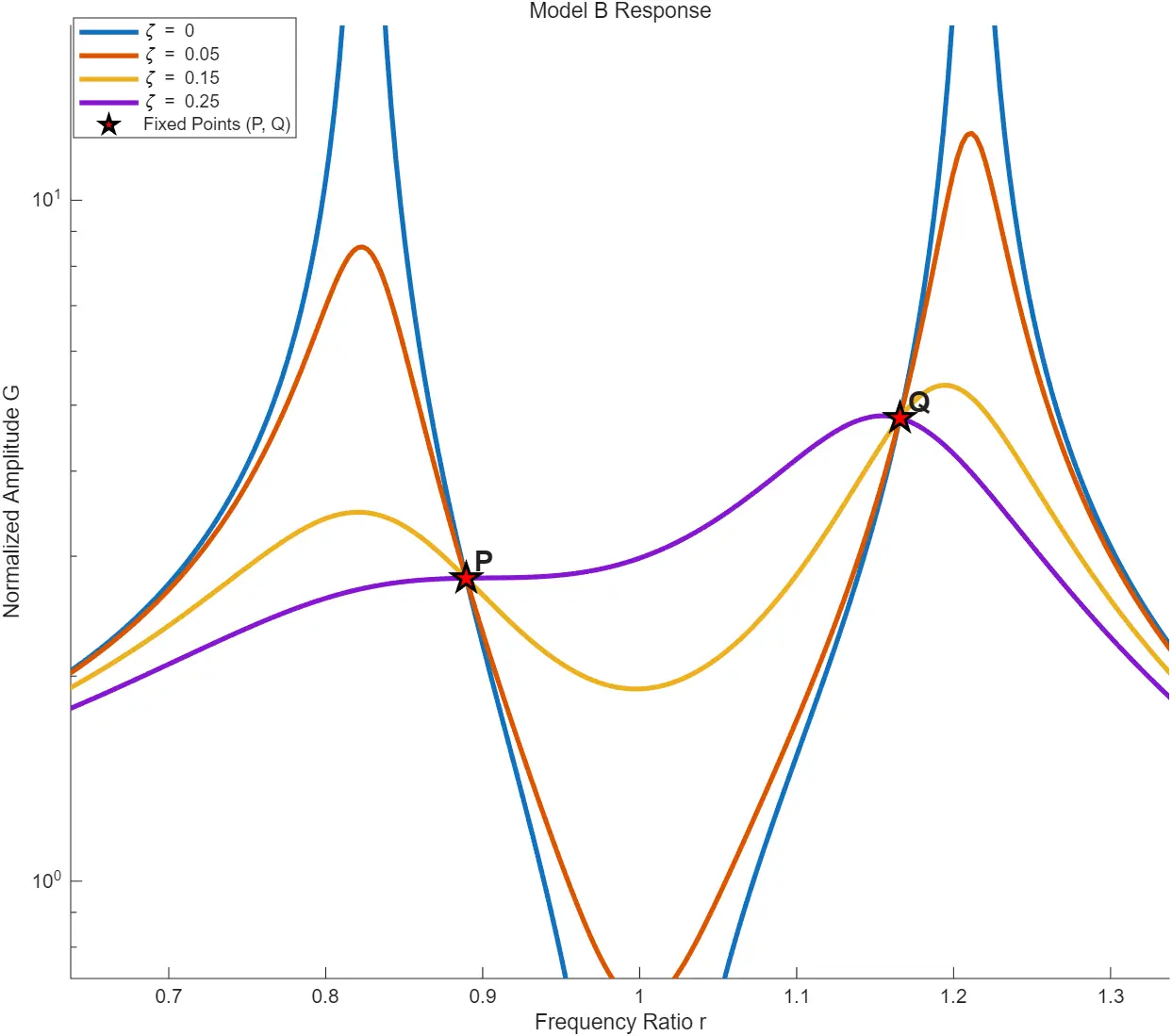
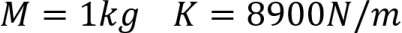
m=0.15kg
给定以下初始条件


分析
无论阻尼比如何变化,曲线恒过P,Q两点
频率比变化会改变固定点的高度
ζ=0
ζ=0.05
ζ=0.15
ζ=0.25
β=1
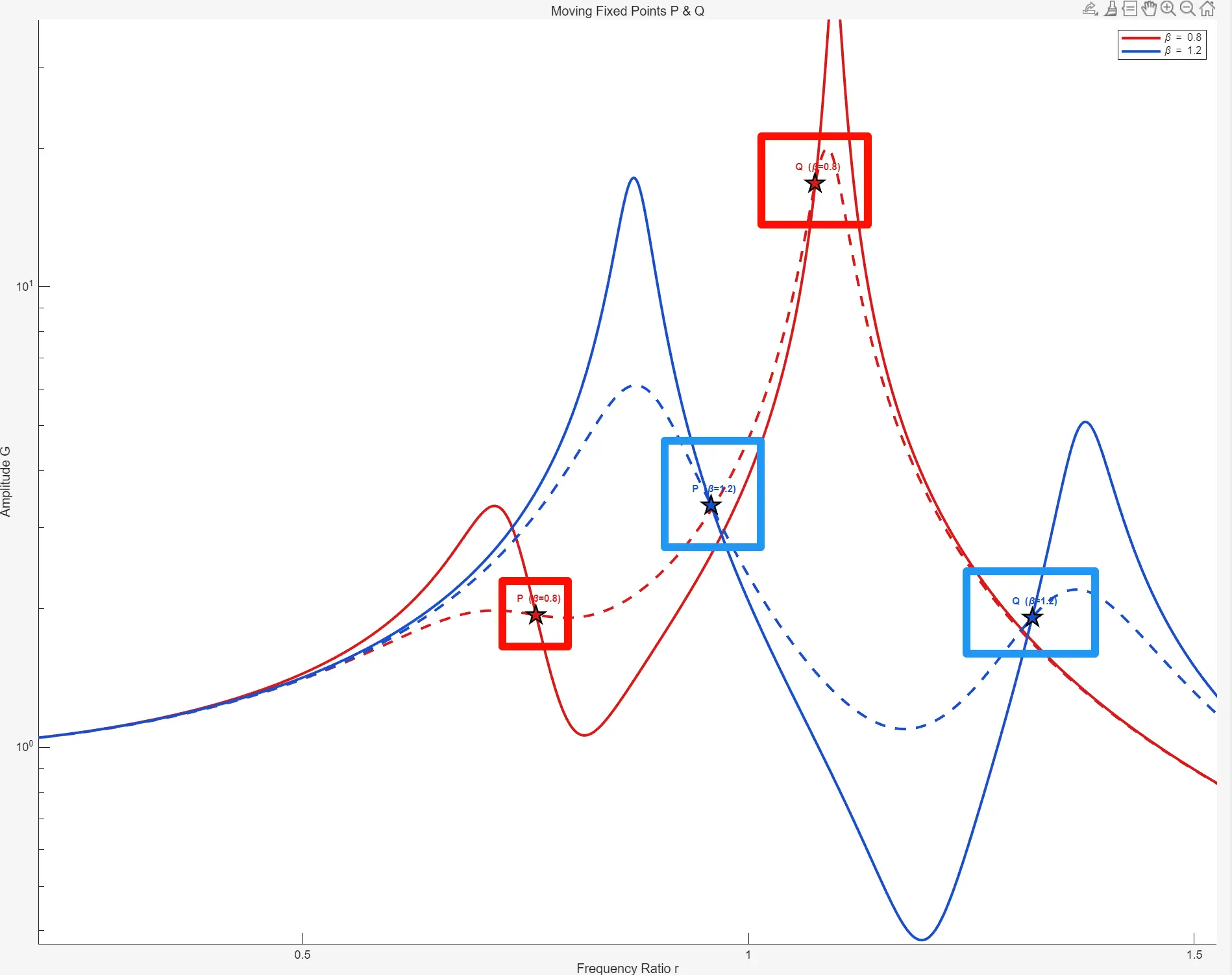
β=1.2
β=0.8




ζ=0.05
ζ=0.05
ζ=0.15
ζ=0.15
结论

调整频率比β使固定点等高
调整阻尼比ζ使曲线水平穿过固定点
为了达到最佳的减振效果
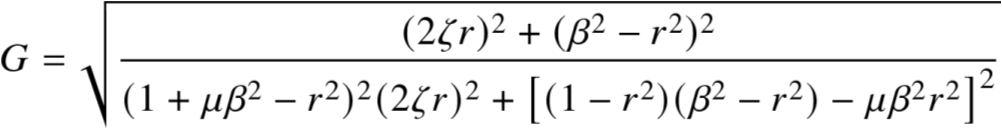

2.3 固定点法求频率比(1/2)
将G改写成以下形式

在固定点P,Q处,G与ζ无关,那么有A/C=B/D
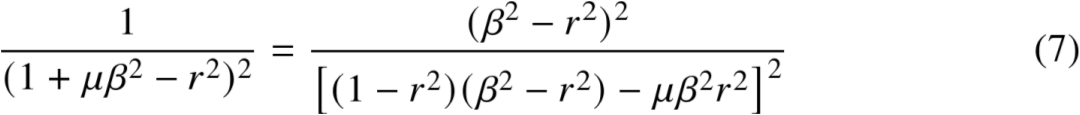
等式两边开方
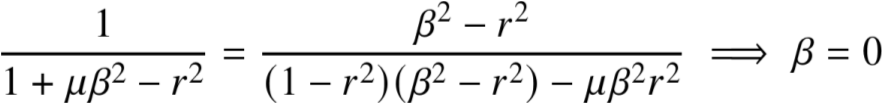

9
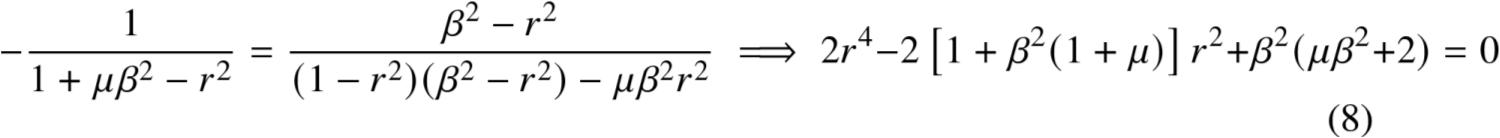
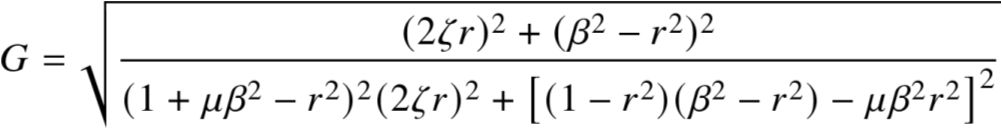
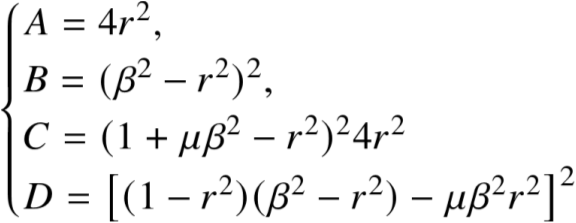

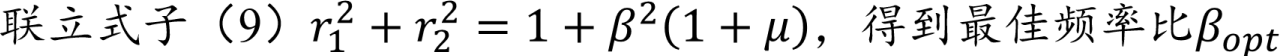
2.3 固定点法求频率比(2/2)
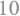
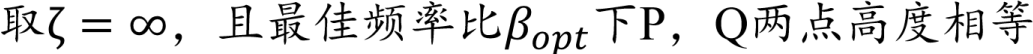
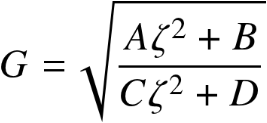
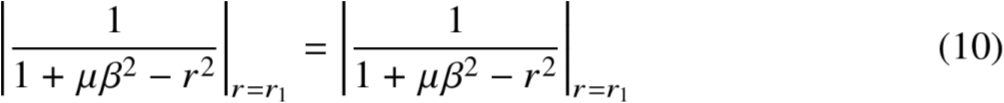
得到式子


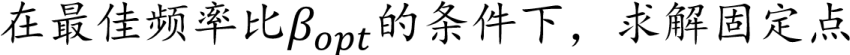
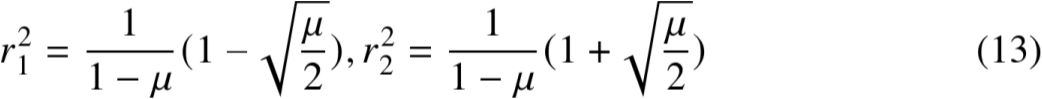
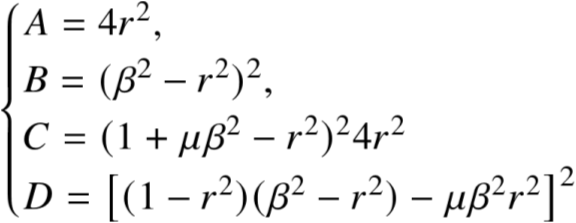

目录
11
01
阻尼动力吸振器
02
最佳频率比
03
最佳阻尼比
04
Matlab程序
05
导数法的补充

3.1 最优阻尼比的定义

最优阻尼比:幅频特性曲线在固定点的切线水平
ζ=0.1
ζ=0.2
ζ=0.3
ζ=0.4

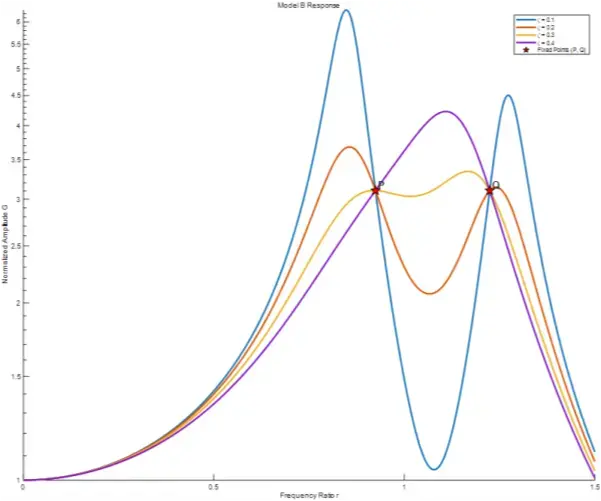
最为直观的求解方法,就是对幅频特性函数求导,令固定点所
在斜率为0,但是计算难度大
Brock提出用微扰法求解,降低了计算难度
最优频率比不同阻尼比的响应曲线

3.2 微扰法(1/3)
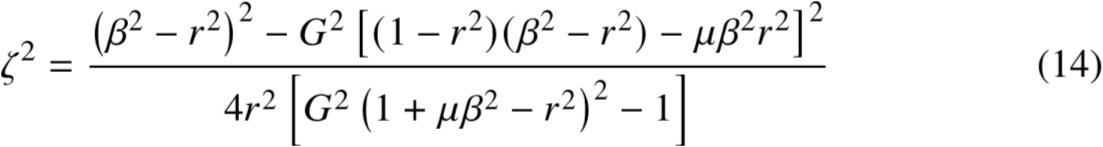
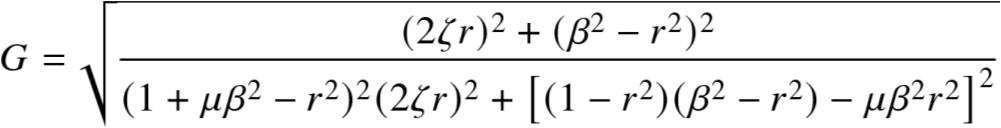
简单地求出ζ的表达式

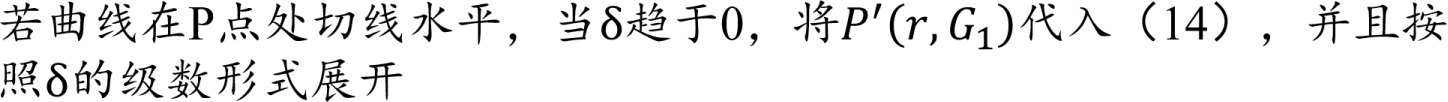
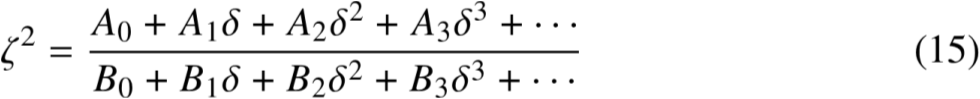

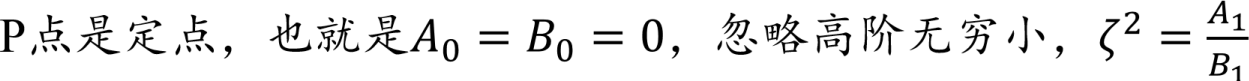

3.2 微扰法(2/3)
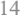

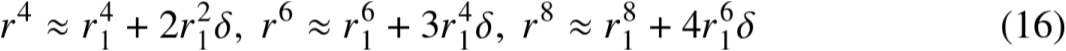
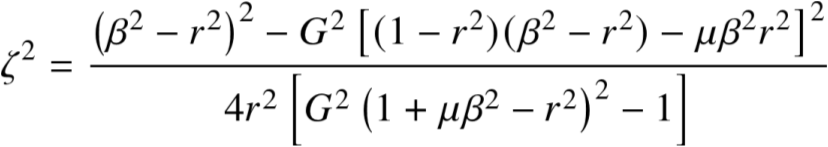

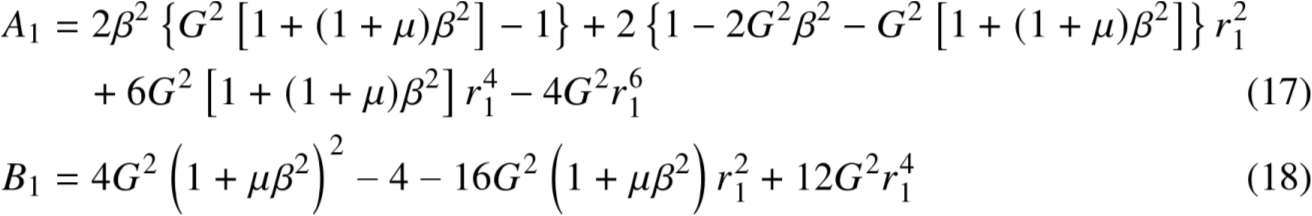
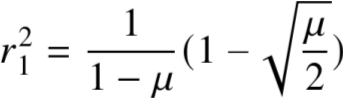
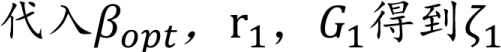
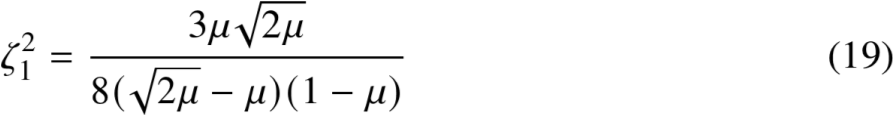

3.2 微扰法(3/3)
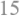
同理,我们可以得到曲线在Q点处切线水平时的ζ值
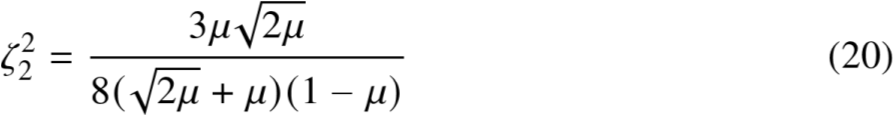
取一个均值,我们得到
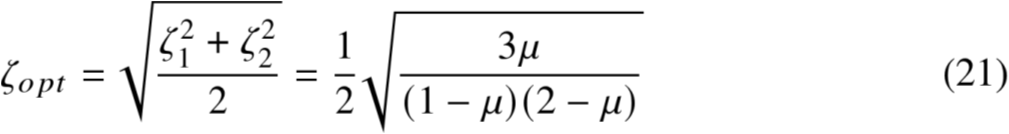

目录
16
01
阻尼动力吸振器
02
最佳频率比
03
最佳阻尼比
04
Matlab程序
05
导数法的补充

4.1 模型对比
17
经典模型
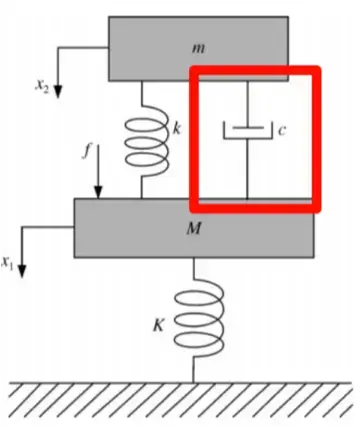
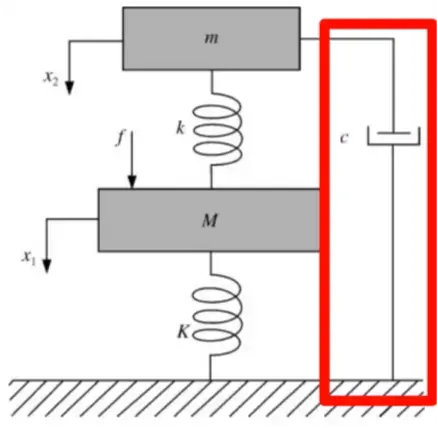
地钩模型
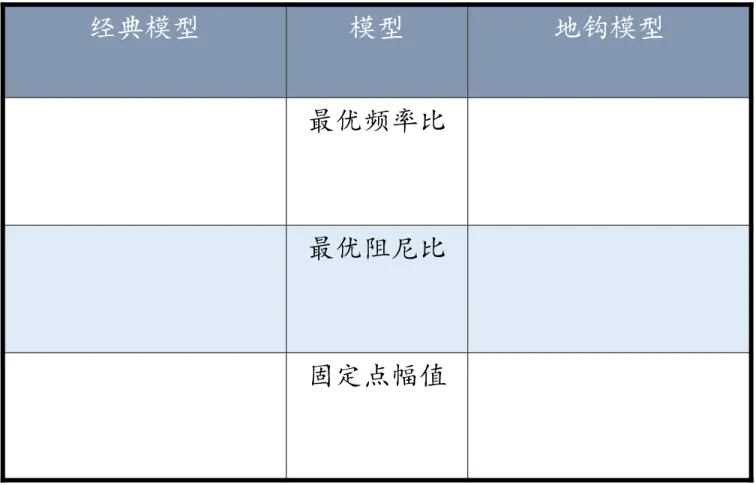
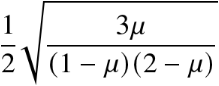

4.2 程序展示
18
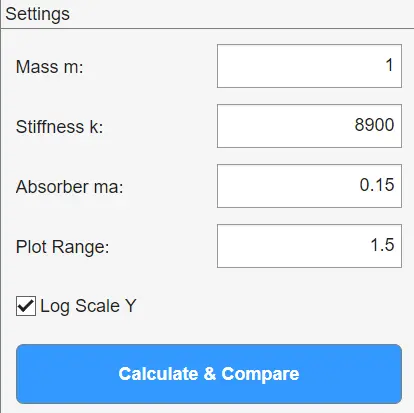
在参数设置区域
可以设置:
1.主系统的质量
2.主质量的刚度
3.吸振器的质量
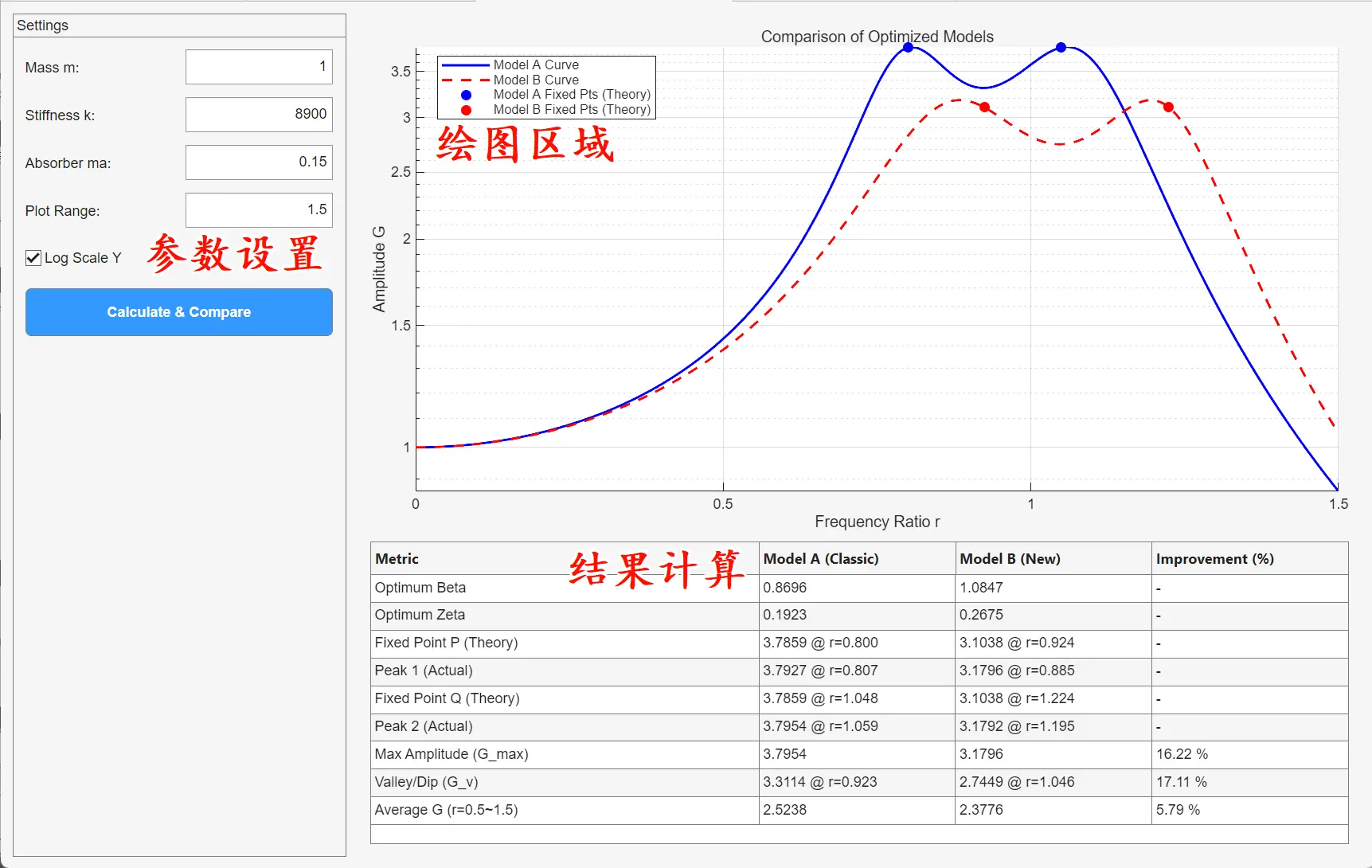
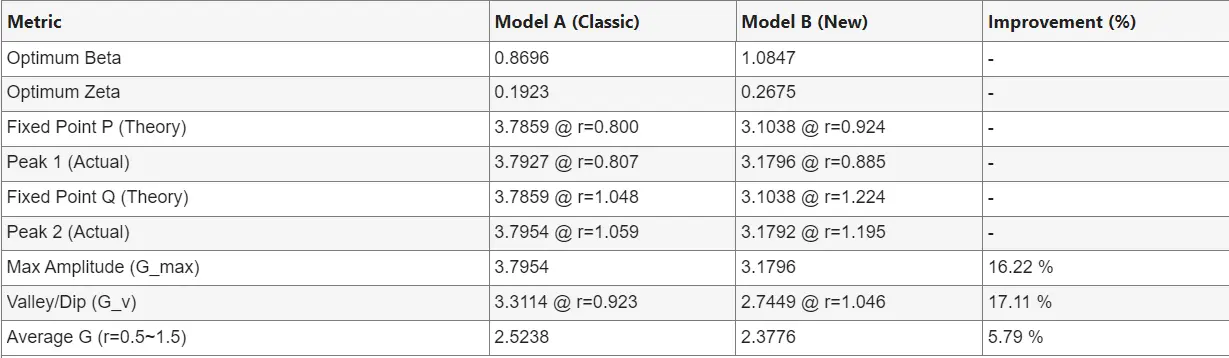
在结果计算区域
程序会计算出经典模型和地钩模型的:
1.最佳频率比和最佳阻尼比
2.固定点P与Q的幅值
3.两个峰值点的幅值
4.幅值的最大峰值
5.幅值的低谷值
6.从0.5到1.5的幅值积分

目录
19
01
阻尼动力吸振器
02
最佳频率比
03
最佳阻尼比
04
Matlab程序
05
导数法的补充

5.1 导数法(1/3)
20
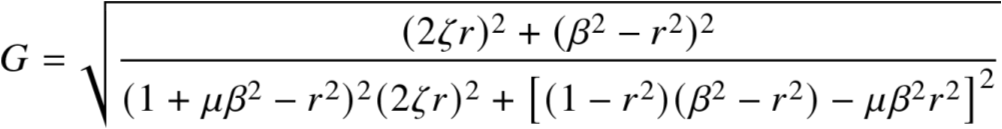
将G写成以下形式
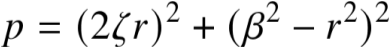
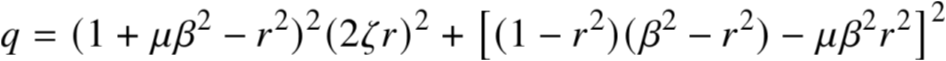
为使曲线在固定点处的斜率为0
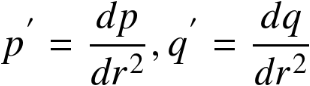

5.1 导数法(2/3)
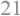
在固定点处
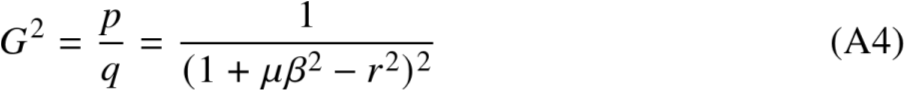
代入(A3) p′q−pq′=0
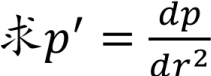

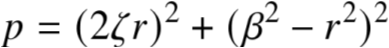
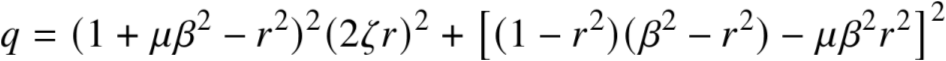
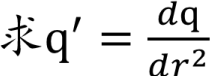
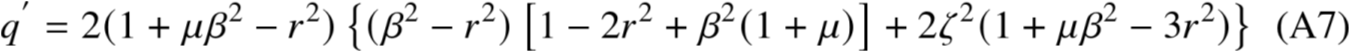

5.1 导数法(3/3)

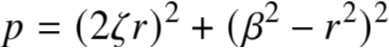
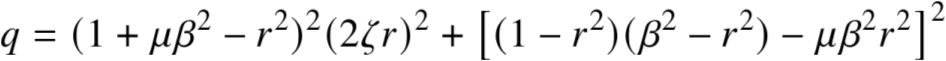
联立A(5),A(6),A(7)
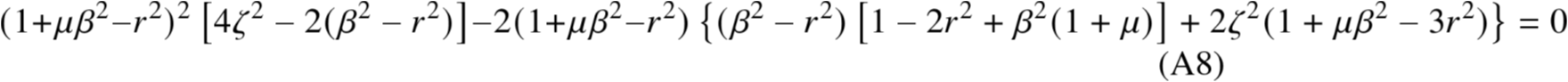
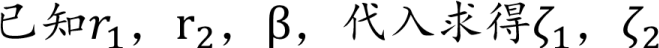
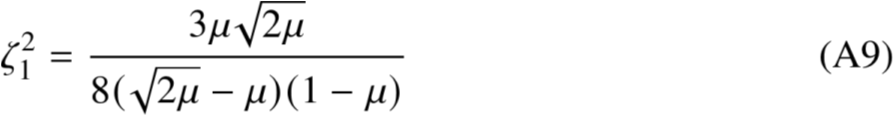
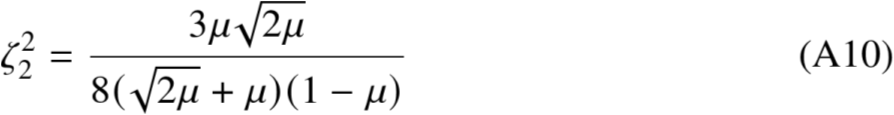
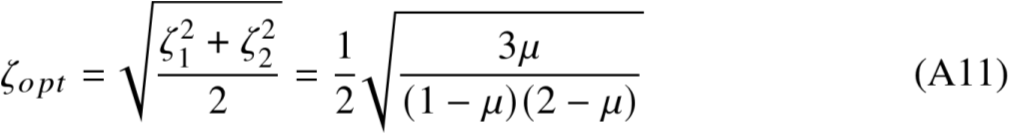

23
谢谢
